UVA 1572 Self-Assembly

发表于 | 分类于 ，

题意：给n个正方形分子，分子的边在一定条件下可以结合，求这些分子能不能形成无穷大的结构。

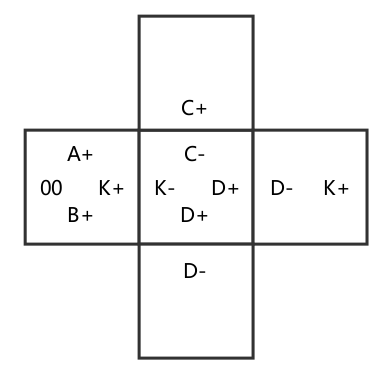
我们从分子的某条边开始铺，假设从下图中的边K+开始铺。K+与K-相结合，再下一步，可以从C-、D+、D+边铺。假设D+与D-相结合后，结合的分子有一条边为K+，那么下一步可以从此K+边开始。问题又回到了起点，按照与之前相同的选择，可以不断重复而组合成无穷大的结构。也就是说，如果从某条边开始，不断地铺，能够到达一条跟它有相同标号的边，那么能够形成无穷大的结构；否则，不能够形成。

考虑以图来建模，把标号作为结点，结点的数目最多有26*2个（不考虑00，因为00不可能在有向圈上）。假设正方形的四条边的标号分别为abcd，记dual(a)表示可以和标号a相结合的标号（如K+和K-可以结合），那么dual(a)可以到达b，dual(b)可以到达a…。问题转化为了找有向图中是否存在有向圈，用拓扑排序可以做。

PS：把dual函数修改了后从50ms到了40ms，rank top 了…

1
2
3
4
5
6
int dual(int v) {
  return (v & 1) ? v - 1 : v + 1;
}
int dual(int v) {
  return v ^= 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>

using namespace std;

const int V = 26 * 2;
const int ID00 = 26 * 2;

int n;
char s[15];
int id[10];
bool G[V][V];
int c[V];

bool dfs(int v) {
  c[v] = 1;
  for (int u = 0; u < V; u++) {
    if (!G[v][u]) continue;
    if (c[u] == 1) return false;
    else if (c[u] == 0 && !dfs(u)) return false;
  }
  c[v] = 2;
  return true;
}

bool solve() {
  memset(c, 0, sizeof(c));
  for (int v = 0; v < V; v++) {
    if (c[v] == 0 && !dfs(v)) return false;
  }
  return true;
}

int dual(int v) {
  return v ^= 1;
}

int main() {
  while (scanf("%d", &n) != EOF) {
    memset(G, 0, sizeof(G));
    for (int i = 0; i < n; i++) {
      scanf("%s", s);
      for (int j = 0; j < 8; j += 2) {
        if (s[j] == '0') id[j / 2] = 26 * 2;
        else id[j / 2] = (s[j] - 'A') * 2 + (s[j + 1] == '+' ? 0 : 1);
      }
      for (int j = 0; j < 4; j++) {
        if (id[j] == ID00) continue;
        int u = dual(id[j]);
        for (int k = 0; k < 4; k++) {
          if (k == j || id[k] == ID00) continue;
          G[u][id[k]] = true;
        }
      }
    }

    printf("%s\n", solve() ? "bounded" : "unbounded");
  }
  return 0;
}