UVA 12171 Sculpture

发表于 | 分类于 ，

题意：给定n个长方体，求这些长方体组合成的物体的表面积和体积。想象组合后的几何体完全浸泡在水中，所求的即为几何体与水接触的面积以及所占据的体积。

可以考虑在坐标系中一个点一个点填充几何体，然后DFS标记出“水区域”。这样，与“水区域”接触的几何体的面积即为所求的表面积，非“水区域”的体积即为所求的体积。因为所给的坐标范围比较大，但n的范围比较小，需要对坐标进行离散化处理。

离散化的一些细节：若所给区间为[x,y]，S为所有坐标点排序后的数组，考虑下面两种：

  1. 离散区间[x,y+1)，写为[x,z)，S中包含的为所有的x和z。考虑两个区间[1,5),[6,11)，填充之后如下图所示，离散坐标i所表示的区间长度为S[i+1]-S[i]，且两个区间中间的部分[5,6)能够表示为未填充的状态。
    图1
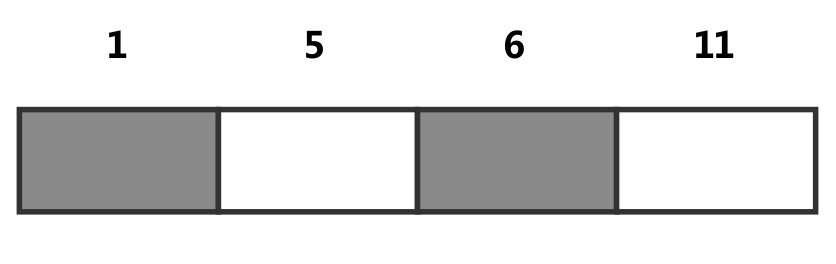
  2. 离散区间[x,y]，S中包含的为所有的x和y。考虑相同的两个区间[1,4],[6,10]，填充之后如下图所示。离散坐标i所表示的区间长度不能统一表示，需要增加一些额外的坐标点来处理。且两个区间中间的部分[5,5]不能表示出状态，也需要增加一些额外的坐标点来处理。

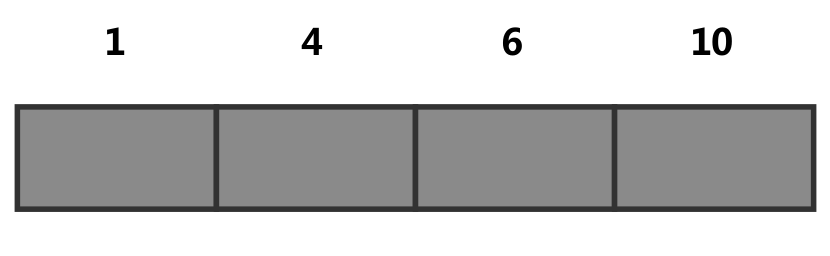
选用第一种离散化的做法，添加0坐标使”水区域“连通。空间坐标\((i,j,k)\)所表示的体积为\((X[i+1]-X[i])*(Y[i+1]-Y[i])*(Z[i+1]-Z[i])\)。

也记一下第二种离散做法遇到的错误。line 99 X[sx++] = X[t] + 1;，最初写的是X[sx++] = X[sx - 2] + 1，没有达到预期的结果，且使得line 22 的assert不成立。没有找到原因，可能是编译的问题，导致数组下标不是所想表示的下标？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 50 + 5;
const int MAX_X = MAX_N * 2;

struct Box { int x0, y0, z0, x, y, z; };

int n;
Box S[MAX_N];
int X[MAX_X], Y[MAX_X], Z[MAX_X], sx, sy, sz;
bool space[MAX_X][MAX_X][MAX_X];
int cmp[MAX_X][MAX_X][MAX_X];

void fill(int x0, int y0, int z0, int x1, int y1, int z1) {
  for (int x = x0; x < x1; x++) {
    for (int y = y0; y < y1; y++) {
      for (int z = z0; z < z1; z++) {
        space[x][y][z] = true;
      }
    }
  }
}

int dx[] = {-1, 1, 0, 0, 0, 0};
int dy[] = {0, 0, -1, 1, 0, 0};
int dz[] = {0, 0, 0, 0, -1, 1};

void dfs(int x, int y, int z) {
  cmp[x][y][z] = 1;
  for (int i = 0; i < 6; i++) {
    int nx = x + dx[i], ny = y + dy[i], nz = z + dz[i];
    if (0 <= nx && nx < sx && 0 <= ny && ny < sy &&
        0 <= nz && nz < sz && !space[nx][ny][nz] && cmp[nx][ny][nz] == 0) {
      dfs(nx, ny, nz);
    }
  }
}

int area() {
  int s = 0;
  for (int i = 0; i < sx; i++) {
    for (int j = 0; j < sy; j++) {
      for (int k = 0; k < sz; k++) {
        if (cmp[i][j][k]) continue;
        for (int m = 0; m < 6; m++) {
          int x = i + dx[m], y = j + dy[m], z = k + dz[m];
          if (cmp[x][y][z]) {
            if (dx[m]) s += (Y[j + 1] - Y[j]) * (Z[k + 1] - Z[k]);
            if (dy[m]) s += (X[i + 1] - X[i]) * (Z[k + 1] - Z[k]);
            if (dz[m]) s += (X[i + 1] - X[i]) * (Y[j + 1] - Y[j]);
          }
        }
      }
    }
  }
  return s;
}

int volume() {
  int s = 0;
  for (int i = 0; i < sx; i++) {
    for (int j = 0; j < sy; j++) {
      for (int k = 0; k < sz; k++) {
        if (cmp[i][j][k]) continue;
        s += (X[i + 1] - X[i]) * (Y[j + 1] - Y[j]) * (Z[k + 1] - Z[k]);
      }
    }
  }
  return s;
}

void discrete(int* X, int& sx) {
  X[sx++] = 0;
  sort(X, X + sx);
  if (sx != 0) {
    int m = 1;
    for (int i = 1; i < sx; i++) {
      if (X[i] != X[i - 1]) X[m++] = X[i];
    }
    sx = m;
  }
}

int main() {
  int T; scanf("%d", &T);
  while (T--) {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      scanf("%d %d %d %d %d %d", &b.x0, &b.y0, &b.z0, &b.x, &b.y, &b.z);
    }
    sx = sy = sz = 0;
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      X[sx++] = b.x0; X[sx++] = b.x0 + b.x;
      Y[sy++] = b.y0; Y[sy++] = b.y0 + b.y;
      Z[sz++] = b.z0; Z[sz++] = b.z0 + b.z;
    }
    discrete(X, sx);
    discrete(Y, sy);
    discrete(Z, sz);

    memset(space, 0, sizeof(space));
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      int x0 = lower_bound(X, X + sx, b.x0) - X;
      int y0 = lower_bound(Y, Y + sy, b.y0) - Y;
      int z0 = lower_bound(Z, Z + sz, b.z0) - Z;
      int x1 = lower_bound(X, X + sx, b.x0 + b.x) - X;
      int y1 = lower_bound(Y, Y + sy, b.y0 + b.y) - Y;
      int z1 = lower_bound(Z, Z + sz, b.z0 + b.z) - Z;
      fill(x0, y0, z0, x1, y1, z1);
    }

    memset(cmp, 0, sizeof(cmp));
    dfs(0, 0, 0);
    printf("%d %d\n", area(), volume());
  }
  return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
#include <bits/stdc++.h>

using namespace std;

const int MAX_N = 50 + 5;
const int MAX_X = MAX_N * 4;

struct Box { int x0, y0, z0, x, y, z; };

int n;
Box S[MAX_N];
int X[MAX_X], Y[MAX_X], Z[MAX_X], sx, sy, sz;
bool space[MAX_X][MAX_X][MAX_X];
int cmp[MAX_X][MAX_X][MAX_X];

void fill(int x0, int y0, int z0, int x1, int y1, int z1) {
  for (int x = x0; x <= x1; x++) {
    for (int y = y0; y <= y1; y++) {
      for (int z = z0; z <= z1; z++) {
        space[x][y][z] = true;
        assert(x >= 1 && y >= 1 && z >= 1);
        assert(x <= sx - 2 && y <= sy - 2 && z <= sz - 2);
//        assert(x >= 1 && x <= sx - 1 && y >= 1 && y <= sy - 1 && z >= 1 && z <= sz - 1);
      }
    }
  }
}

int dx[] = {-1, 1, 0, 0, 0, 0};
int dy[] = {0, 0, -1, 1, 0, 0};
int dz[] = {0, 0, 0, 0, -1, 1};

void dfs(int x, int y, int z) {
  cmp[x][y][z] = 1;
  for (int i = 0; i < 6; i++) {
    int nx = x + dx[i], ny = y + dy[i], nz = z + dz[i];
    if (0 <= nx && nx < sx && 0 <= ny && ny < sy &&
        0 <= nz && nz < sz && !space[nx][ny][nz] && cmp[nx][ny][nz] == 0) {
      dfs(nx, ny, nz);
    }
  }
}

int area() {
  int s = 0;
  for (int i = 0; i < sx; i++) {
    for (int j = 0; j < sy; j++) {
      for (int k = 0; k < sz; k++) {
        if (cmp[i][j][k]) continue;
        for (int m = 0; m < 6; m++) {
          int x = i + dx[m], y = j + dy[m], z = k + dz[m];
          if (cmp[x][y][z]) {
//            assert(i + 1 < sx);
//            assert(j + 1 < sy);
//            assert(k + 1 < sz);
            if (dx[m]) s += (Y[j + 1] - Y[j]) * (Z[k + 1] - Z[k]);
            if (dy[m]) s += (X[i + 1] - X[i]) * (Z[k + 1] - Z[k]);
            if (dz[m]) s += (X[i + 1] - X[i]) * (Y[j + 1] - Y[j]);
          }
        }
      }
    }
  }
  return s;
}

int volume() {
  int s = 0;
  for (int i = 0; i < sx; i++) {
    for (int j = 0; j < sy; j++) {
      for (int k = 0; k < sz; k++) {
        if (cmp[i][j][k]) continue;
//        assert(i + 1 < sx);
//        assert(j + 1 < sy);
//        assert(k + 1 < sz);
        s += (X[i + 1] - X[i]) * (Y[j + 1] - Y[j]) * (Z[k + 1] - Z[k]);
      }
    }
  }
  return s;
}

void discrete(int* X, int& sx) {
  X[sx++] = 0;
  sort(X, X + sx);
  if (sx != 0) {
    int m = 1;
    for (int i = 1; i < sx; i++) {
      if (X[i] != X[i - 1]) X[m++] = X[i];
    }
    sx = m;
  }
  for (int i = sx - 2; i >= 0; i--) {
    if (X[i + 1] != X[i] + 1) X[sx++] = X[i] + 1;
  }
  sort(X, X + sx);
  int t = sx - 1;
  assert(sx >= 1);
  X[sx++] = X[t] + 1; // adding a boundary, for convenience
}

int main() {
  int T; scanf("%d", &T);
  while (T--) {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      scanf("%d %d %d %d %d %d", &b.x0, &b.y0, &b.z0, &b.x, &b.y, &b.z);
    }
    sx = sy = sz = 0;
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      X[sx++] = b.x0; X[sx++] = b.x0 + b.x - 1;
      Y[sy++] = b.y0; Y[sy++] = b.y0 + b.y - 1;
      Z[sz++] = b.z0; Z[sz++] = b.z0 + b.z - 1;
    }
    discrete(X, sx);
    discrete(Y, sy);
    discrete(Z, sz);

//    for (int i = 0; i < sx; i++) cout << X[i] << ' '; cout << endl;
//    for (int i = 0; i < sy; i++) cout << Y[i] << ' '; cout << endl;
//    for (int i = 0; i < sz; i++) cout << Z[i] << ' '; cout << endl;
    memset(space, 0, sizeof(space));
    for (int i = 0; i < n; i++) {
      Box& b = S[i];
      int x0 = lower_bound(X, X + sx, b.x0) - X;
      int y0 = lower_bound(Y, Y + sy, b.y0) - Y;
      int z0 = lower_bound(Z, Z + sz, b.z0) - Z;
      int x1 = lower_bound(X, X + sx, b.x0 + b.x - 1) - X;
      int y1 = lower_bound(Y, Y + sy, b.y0 + b.y - 1) - Y;
      int z1 = lower_bound(Z, Z + sz, b.z0 + b.z - 1) - Z;
//      printf("%d %d %d %d %d %d\n", x0, y0, z0, x1, y1, z1);
      fill(x0, y0, z0, x1, y1, z1);
    }

    memset(cmp, 0, sizeof(cmp));
    dfs(0, 0, 0);
    printf("%d %d\n", area(), volume());
  }
  return 0;
}