Link Cut Tree

发表于 | 分类于 ， ，

LCT用来维护有根树的森林。对任意结点v，Preferred Child（PC）的定义为：如果v没被访问过或者刚刚访问到v，则PC[v] = null；如果刚刚访问到v的孩子结点u所在的子树，则PC[v] = u。v到其preferred child（如果有）的边为preferred edge，preferred edge连接起来形成preferred path。需要表示的树（也就是直观上的树）称为represented tree。LCT把每一条preferred path维护成一个树，称为Auxiliary Tree，所用的数据结构为Splay Tree。

树链剖分是Heavy Light Decomposition，把一个结点的孩子分为重和轻，是按照树的结构来进行划分。LCT是Preferred Path Decomposition，是按照对结点的访问来划分的。

借用MIT 6.851课件的图：

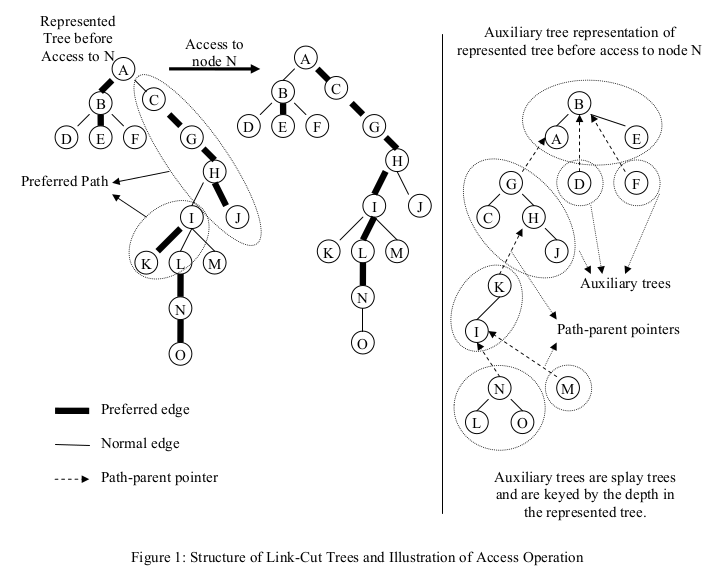
LCT的基本操作为access(v),make_root(v),link(v,w),cut(v,w)
in represented tree world:
access(v)把从根结点到v的路径变为preferred path
make_root(v)把v变为所在有根树的根结点
link(v,w)v是所在树的根结点，连接v和w
cut(v,w)去掉v和w之间的边

in Aux tree world:
实现上 见代码>,<
每个操作的复杂度为O(logn)，证明？

在每一个splay树中，相当于是把结点深度作为键值，进行中序遍历可得到从最接近根的结点到深度最大的结点的路径，即一条preferred path所对应的结点。
access(v)把根结点到v的路径上的所有结点放在一颗splay树中，如果维护路径上的信息，则可在这颗splay树的根结点获得统计信息。
如果要得到u到v的路径上的统计信息，可以先make_root(u)把u变为有根树的根结点，再access(v)把u到v的路径上的所有结点放在一个splay树中。
LCT是来解决动态树问题的，也就是树的结构在发生变化，不断有边的加入或边的消去。在树的结构发生变化的条件下树链剖分不太能做。

UOJ 3 魔法森林
按照A的值排序所有的边，按照排好的顺序依次向图中加入边，图中每条边的权值为此边的B值。加边的规则为：设边e的两端点是(u,v)，如果u,v不连通则加入e；如果连通，则查询u到v的路径上的最大权值b，如果b>e.B，则去掉u->v路径上最大权值的边，加入e，否则不加入e。

每加入一条边e，查询1和N是否连通，如果连通则求出1到N的路径上最大权值，所求结果1->N的路径所对应的值（即最大A值+最大B值）r=min（e.A+1->N路径上的最大权值）。

证明：
按照加入边的规则，保证任意一对结点之间最多只有一条路径，也就是在加边的过程中，这个图是一个森林。

证明在加入边e之后的森林中1->N的路径所对应的值为min（e.A+1->N路径上的最大权值）：
如果加入e之前1->N不连通，加入e之后连通则1->N的路径上必包含e，此条路径所对应的值为（e.A+1->N路径上的最大权值）。
如果加入e之前1->N已经连通，加入e后，如果1->N的路径上包含e，则此条路径所对应的值为（e.A+1->N路径上的最大权值）。如果1->N的路径上不包含e，则（e.A+1->N路径上的最大权值）>=（e1.A+1->N路径上的最大权值），e1为1->N的路径上A值最大的边，e1在e之前加入，有e.A>=e1.A，则此次更新不影响结果。

粗略证明加边策略的正确性：
任意两点之间的最大权值尽可能小，这样才能使1->N路径上的最大权值尽可能减少，才能使1->N的路径所对应的值尽可能减少。

实现上，因为所维护的值在顶点上，把一条边作为一个顶点w，加入边e(u,v)时加入w->u和w->v两条边，去边e(u,v)时也是去两条。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
#include <iostream>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <string>
#include <algorithm>
#include <functional>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>

using namespace std;
const int MAX_N = 50000 + 10;
const int MAX_M = 100000 + 10;
const int INF = ~0U >> 1;
int N, M;
struct Edge {
  int u, v, A, B;
} es[MAX_M];
bool comp(const Edge& e1, const Edge& e2) {
  return e1.A < e2.A;
}

// union set
int par[MAX_N], rank[MAX_N];
int find(int x) {
  if (x == par[x]) return x;
  else return par[x] = find(par[x]);
}
bool same(int x, int y) {
  return find(x) == find(y);
}
void unite(int x, int y) {
  x = find(x);
  y = find(y);
  if (rank[x] < rank[y]) {
    par[x] = y;
  } else {
    par[y] = x;
    if (rank[x] == rank[y]) rank[x]++;
  }
}

// LCT
struct Node {
  Node *p, *ch[2];
  int val, id, mx, mxid, rev, size;
  Node() {
    val = 0;
    rev = 0;
    size = 0;
  }
  int d() {
    return this == p->ch[1];
  }
  void setc(Node* c, int d) {
    ch[d] = c;
    c->p = this;
  }
  void revIt() {
    rev ^= 1;
    swap(ch[0], ch[1]);
  }
  bool is_root() {
    return p->ch[0] != this && p->ch[1] != this;
  }
  void push_up() {
    mx = val;
    mxid = id;
    for (int i = 0; i < 2; i++) {
      if (ch[i]->mx > mx) {
        mx = ch[i]->mx;
        mxid = ch[i]->mxid;
      }
    }
    size = ch[0]->size + ch[1]->size + 1;
  }
  void push_down() {
    if (rev) {
      ch[0]->revIt();
      ch[1]->revIt();
      rev = 0;
    }
  }
} Tnull, *null = &Tnull;
Node npool[MAX_N + MAX_M], *V[MAX_N + MAX_M];

void init() {
  for (int i = 1; i <= N; i++) {
    par[i] = i;
    rank[i] = 0;
  }

  for (int i = 1; i <= N + M; i++) {
    Node* v = npool + i;
    V[i] = v;
    v->p = null;
    v->ch[0] = null;
    v->ch[1] = null;
    v->val = i > N ? es[i - N].B : 0; 
    v->id = i > N ? i - N : 0;
    v->mx = v->val;
    v->mxid = v->id;
    v->rev = 0;
  }
}

void rotate(Node* x) {
  Node* p = x->p;
  int d = x->d();
  p->push_down();
  x->push_down();
  if (p->is_root()) {
    x->p = p->p;
  } else {
    p->p->setc(x, p->d());
  }
  p->setc(x->ch[!d], d);
  x->setc(p, !d);
  p->push_up();
  // x->push_up();
}

void splay(Node* x) {
  x->push_down();
  while (!x->is_root()) {
    if (x->p->is_root()) {
      rotate(x);
    } else {
      x->d() == x->p->d() ? rotate(x->p) : rotate(x);
      rotate(x);
    }
  }
  x->push_up();
}

void access(Node* v) {
  Node* t = null;
  while (v != null) {
    splay(v);
    v->ch[1] = t;
    v->push_up();
    t = v;
    v = v->p;
  }
}

void make_root(Node* v) {
  access(v);
  splay(v);
  v->revIt();
}

void link(Node* v, Node* u) {
  make_root(v);
  v->p = u;
}

void cut(Node* v, Node* u) {
  make_root(v);
  access(u);
  splay(u);
  v->p = null;
  u->ch[0] = null;
  u->push_up();
}

Node* query(Node* v, Node* u) {
  make_root(v);
  access(u);
  splay(u);
  return u;
}

int main() {
  scanf("%d %d", &N, &M);
  for (int i = 1; i <= M; i++) {
    int u, v, A, B;
    scanf("%d %d %d %d", &u, &v, &A, &B);
    es[i] = (Edge){u, v, A, B};
  }
  sort(es + 1, es + M + 1, comp);
  init();
  int res = INF;
  for (int i = 1; i <= M; i++) {
    Edge& e = es[i];
    int u = e.u, v = e.v;
    if (same(u, v)) {
      Node* q = query(V[u], V[v]);
      if (q->mx > e.B) {
        // cause q->mxid maybe changed in cut and link ops
        int mxid = q->mxid;
        Edge& e1 = es[mxid];
        int u1 = e1.u, v1 = e1.v;
        cut(V[u1], V[N + mxid]);
        cut(V[v1], V[N + mxid]);
        link(V[u], V[N + i]);
        link(V[v], V[N + i]);
      }
    } else {
      unite(u, v);
      link(V[u], V[N + i]);
      link(V[v], V[N + i]);
    }
    if (same(1, N)) {
      // query path from 1 to N
      res = min(res, e.A + query(V[1], V[N])->mx);
    }
  }
  printf("%d\n", res == INF ? -1 : res);
  return 0;
}

BZOJ 2049 Cave 洞穴勘测
LCT模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
    Result: Accepted
    Time:1632 ms
    Memory:1488 kb
****************************************************************/
 
#include <iostream>
#include <vector>
#include <string>
#include <set>
#include <map>
#include <algorithm>
#include <functional>
#include <stack>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
 
using namespace std;
 
const int MAX_N = 10000 + 10;
 
int n, m;
 
struct Node {
  Node *p, *ch[2];
  int rev;
  Node() {
    rev = 0;
  }
  bool d() {
    return this == p->ch[1];
  }
  void setc(Node* c, int d) {
    ch[d] = c;
    c->p = this;
  }
  void revIt() {
    rev ^= 1;
  }
  bool is_root();
  void push_up() {
 
  }
  void push_down() {
    if (rev) {
      this->revIt();
      ch[0]->revIt();
      ch[1]->revIt();
      swap(ch[0], ch[1]);
    }
  }
} Tnull, *null = &Tnull;
Node mem[MAX_N], *C = mem, *V[MAX_N];
bool Node::is_root() {
  // return p->ch[0] != this && p->ch[1] != this;
  return p == null || (p->ch[0] != this && p->ch[1] != this);
}
Node* new_node() {
  C->p = null;
  C->ch[0] = null;
  C->ch[1] = null;
  C->rev = 0;
  return C++;
}
 
void build() {
  for (int i = 1; i <= n; i++) {
    V[i] = new_node();
  }
}
 
void rotate(Node* x) {
  Node* p = x->p;
  p->push_down();
  x->push_down();
  int d = x->d();
  if (p->is_root()) {
    x->p = p->p;
  } else {
    p->p->setc(x, p->d());
  }
  p->setc(x->ch[!d], d);
  x->setc(p, !d);
  p->push_up();
  // x->push_up();
}
 
void splay(Node* x) {
  x->push_down();
  while (!x->is_root()) {
    if (x->p->is_root()) {
      rotate(x);
    } else {
      x->d() == x->p->d() ? rotate(x->p) : rotate(x);
      rotate(x);
    }
  }
  x->push_up();
}
 
void access(Node* v) {
  Node* t = null;
  while (v != null) {
    splay(v);
    v->ch[1] = t;
    v->push_up();
    t = v;
    v = v->p;
  }
}
 
void make_root(Node* v) {
  access(v);
  splay(v);
  v->revIt();
}
 
Node* find_root(Node* v) {
  access(v);
  splay(v);
  Node* r = v;
  while (r->ch[0] != null) r = r->ch[0];
  splay(r);
  return r;
}
 
void link(Node* v, Node* w) {
  make_root(v);
  // if (find_root(w) == v) return;
  v->p = w;
}
 
void cut(Node* v, Node* u) {
  make_root(v);
  // if (find_root(u) != v) return;
  access(u);
  splay(u);
  v->p = null;
  u->ch[0] = null;
  u->push_up();
}
 
bool query(Node* v, Node* u) {
  return find_root(v) == find_root(u);
}
 
int main() {
  scanf("%d %d", &n, &m);
  build();
  for (int i = 0; i < m; i++) {
    char cmd[10];
    int u, v;
    scanf("%s %d %d", cmd, &u, &v);
    if (cmd[0] == 'Q') {
      printf("%s\n", query(V[u], V[v]) ? "Yes" : "No");
    } else if (cmd[0] == 'C') {
      // if u v already connect
      link(V[u], V[v]);
    } else {
      // if u v don't connect
      cut(V[u], V[v]);
    }
  }
  return 0;
}